https://www.acmicpc.net/problem/11658
11658번: 구간 합 구하기 3
첫째 줄에 표의 크기 N과 수행해야 하는 연산의 수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는
www.acmicpc.net

[ 문제풀이 ]
이 문제를 풀기 전에 다음 글을 먼저 읽고 오시는 것을 추천드립니다.
https://rudalsd.tistory.com/51
[ 자료구조 ] 세그먼트 트리 (Segment Tree)
1. 세그먼트 트리 (Segment Tree) 먼저, 세그먼트 트리가 무엇인지 알아봅시다! 세그먼트 트리는 구간 합을 저장하기 위한 트리입니다. 예를 들어 size가 5인 배열이 있다고 생각해봅시다. int arr [5] = {1
rudalsd.tistory.com
1. 이 문제를 풀기 위해서 2차원 세그먼트 트리를 만듭니다. (segTree [ x ][ y ])
2. segTree[ x ]의 리프노드에 x행의 값들을 다시 세그먼트 트리의 형식으로 저장합니다.
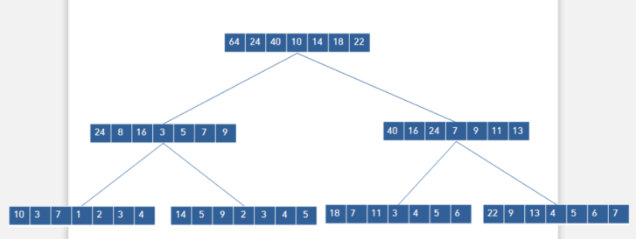
3. 특정 좌표의 값을 업데이트할 때 x행의 세그먼트 트리 노드를 찾은 후 y열의 세그먼트 트리 노드 값을 바꿔줍니다.
4. 구간 합을 구할 때도 3과 마찬가지로 x행의 세그먼트 트리 노드를 찾은 후 y열의 세그먼트 트리 노드의 구간합을 구해줍니다.
[ 소스코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 | #include<iostream> using namespace std; int N, M; int segTree[2050][2050]; int arr[1025][1025]; void updateTreeY(int node, int s, int e, int x, int y, int diff) { if (y < s || e < y) return; segTree[x][node] += diff; if (s != e) { int m = (s + e) / 2; updateTreeY(node * 2, s, m, x, y, diff); updateTreeY(node * 2+1, m+1, e, x, y, diff); } } void updateTreeX(int node, int s, int e, int x, int y, int diff) { if (x < s || e < x) return; updateTreeY(1, 1, N, node, y, diff); if (s != e) { int m = (s + e) / 2; updateTreeX(node * 2, s, m, x, y, diff); updateTreeX(node * 2 + 1, m + 1, e, x, y, diff); } } int sumTreeY(int node, int s, int e, int x, int y1, int y2) { if (y2 < s || e < y1) return 0; if (y1 <= s && e <= y2) return segTree[x][node]; int m = (s + e) / 2; int left = sumTreeY(node * 2, s, m, x, y1, y2); int right = sumTreeY(node * 2 + 1, m + 1, e, x, y1, y2); return left + right; } int sumTreeX(int node, int s, int e, int x1, int y1, int x2, int y2) { if (x2 < s || e < x1) return 0; if (x1 <= s && e <= x2) return sumTreeY(1, 1, N, node, y1, y2); int m = (s + e) / 2; int left = sumTreeX(node * 2, s, m, x1, y1, x2, y2); int right = sumTreeX(node * 2 + 1, m + 1, e, x1, y1, x2, y2); return left + right; } int main() { scanf("%d %d", &N, &M); for (int i = 1; i <= N; i++) { for (int j = 1; j <= N; j++) { scanf("%d", &arr[i][j]); updateTreeX(1, 1, N, i, j, arr[i][j]); } } for (int i = 0; i < M; i++) { int w; scanf("%d", &w); if (w == 0) { int x, y, c; scanf("%d %d %d", &x, &y, &c); int diff = c - arr[x][y]; arr[x][y] = c; updateTreeX(1, 1, N, x, y, diff); } else { int ans = 0; int x1, y1, x2, y2; scanf("%d %d %d %d", &x1, &y1, &x2, &y2); printf("%d\n", sumTreeX(1, 1, N, x1, y1, x2, y2)); } } } | cs |
'백준' 카테고리의 다른 글
| [ 백준 ] 15971번 - 두 로봇 (C++) (0) | 2023.02.10 |
|---|---|
| [ 백준 ] 2637번 - 장난감 조립 (C++) (0) | 2023.02.09 |
| [ 백준 ] 2458번 - 키 순서 (C++) (0) | 2023.02.07 |
| [ 백준 ] 2211번 - 네트워크 복구 (C++) (0) | 2023.02.06 |
| [ 백준 ] 17835번 - 면접보는 승범이네 (C++) (0) | 2023.02.05 |