반응형
오늘 설명할 알고리즘은 플로이드 와샬 알고리즘(Floyd Warshall Algorithm)입니다. 이 알고리즘은 dijkstra와 비슷하게 각 정점까지 가는 최단 거리를 알아낼 수 있습니다. 플로이드 와샬 알고리즘이 dijkstra보다 시간은 더 오래 걸리지만 모든 노드들 간의 최단 거리를 알아낼 수 있습니다.
[ 동작 원리 ]
- 시작 정점, 중간에 거쳐갈 정점 그리고 도착 정점을 선택합니다.
- 만약 시작 정점부터 도착 정점까지 거리보다 시작 정점 - 중간 정점 - 도착 정점까지의 거리가 더 짧다면 값을 경신시켜줍니다.
플로이드 와샬 알고리즘의 동작 과정을 그림으로 이해해 봅시다.
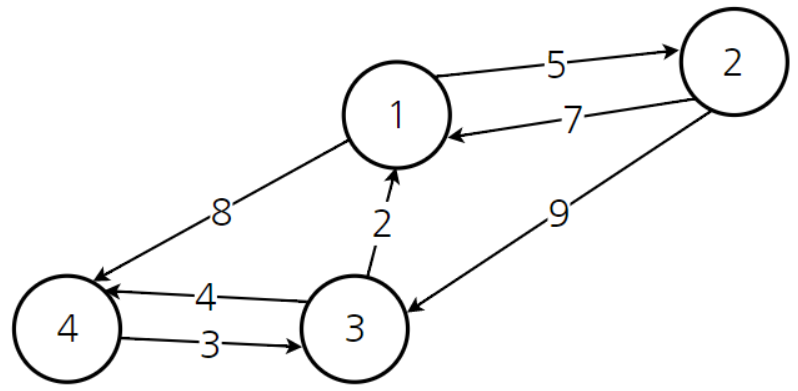
위와 같은 그래프가 존재할 때 각 정점에서부터 정점에서까지의 거리를 2차원 배열로 나타내면 다음과 같습니다.

위의 2차원 배열이 나타내는 것은 바로 현재까지 계산된 각 노드에서 노드까지의 최소 비용입니다. 이를 3중 for문을 이용하여 모든 노드들에 대해 값을 경신해나가면 마지막에는 특정 노드에서 노드까지의 최소 비용을 모두 구할 수 있습니다.
먼저 노드 1을 거쳐가는 경우는 다음과 같습니다.
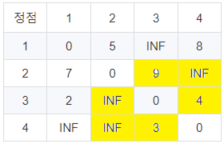
노드 1을 거쳐가는 경우에는 위의 6개의 값만 경신시켜주면 됩니다. 이때 시작 노드와 도착 노드까지의 거리와 시작 노드 - 중간 노드 - 도착 노드까지의 거리 중 더 짧은 거리로 갱신시켜주면 됩니다.
위의 과정을 거치면 다음과 같은 결과를 얻을 수 있습니다.

이런 방법으로 1번부터 4번 노드까지 모두 값을 갱신해주면 다음과 같은 결과를 얻을 수 있습니다.
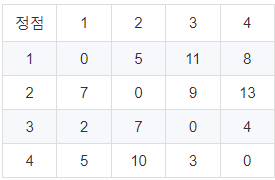
[ 소스 코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | #include <iostream> using namespace std; int n, m; long long cost[101][101]; int main() { cin >> n >> m; for (int i = 1; i <= n; i++) { //출발지와 도착지가 같을 때 0으로 초기화 for (int j = 1; j <= n; j++) { //아니라면 INF로 초기화 if (i == j) { cost[i][j] = 0; } else { cost[i][j] = 99999999999; } } } for (int i = 0; i < m; i++) { //출발지와 도착지가 같은 간선이 여러개일 때 int a, b, c; //가장 짧은 거리로 초기화 scanf("%d %d %d", &a, &b, &c); if (cost[a][b] > c) { cost[a][b] = c; } } for (int k = 1; k <= n; k++) { //거쳐가는 노드 for (int i = 1; i <= n; i++) { //출발 노드 for (int j = 1; j <= n; j++) { //도착 노드 if (cost[i][j] > cost[i][k] + cost[k][j]) { cost[i][j] = cost[i][k] + cost[k][j]; } } } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { cout << cost[i][j] << " "; } cout << endl; } } | cs |
반응형
'알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] 오일러 피 함수(Euler's phi function) (0) | 2022.07.09 |
|---|---|
| [ 알고리즘 ] 포함 배제의 원리(Inclusion–exclusion principle) (0) | 2022.06.30 |
| [ 알고리즘 ] 모듈러 연산(Modular Arithmetic) (0) | 2022.06.29 |
| [ 알고리즘 ] 외판원 순회 알고리즘(Traveling Salesperson Problem, TSP) (0) | 2022.06.21 |
| [ 알고리즘 ] 벨만 포드 알고리즘(Bellman-Ford Algorithm) (0) | 2022.06.08 |