1. 세그먼트 트리 (Segment Tree)
먼저, 세그먼트 트리가 무엇인지 알아봅시다! 세그먼트 트리는 구간 합을 저장하기 위한 트리입니다. 예를 들어 size가 5인 배열이 있다고 생각해봅시다. int arr [5] = {1,2,3,4,5} 일 때, 다음과 같은 그래프로 나타낼 수 있습니다.
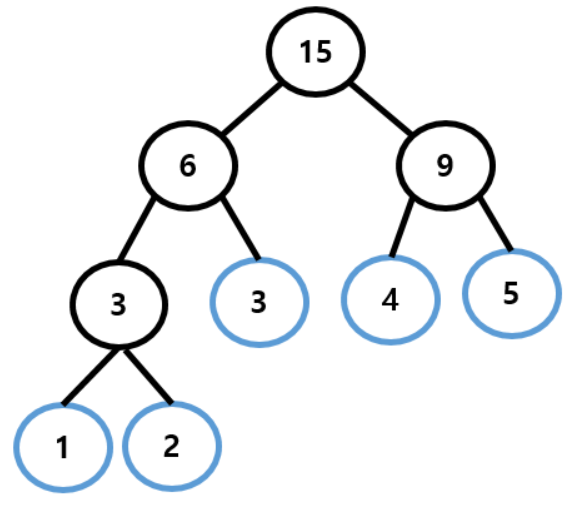
각각의 노드들의 값은 자식 노드들의 값들을 더한 것입니다. 구간의 합을 구할 때 보통 O(N)의 시간이 걸리지만 세그먼트 트리를 이용한다면 O(logN)의 시간만에 값을 구할 수 있습니다.
트리를 만들기 위해서는 트리의 높이를 알아야 합니다. 트리의 높이를 알기 위해서는 리프노드의 수를 이용해야 하고, 다음과 같이 구할 수 있습니다.
트리의 높이 = ceil(log(N))
ceil은 어떤 수든 올림을 해서 구해주는 함수입니다. 따라서 log5 = 2.xxx이지만 ceil함수 안에 넣는다면 3이라는 수가 나오게 됩니다. 위의 그래프를 보면 루트 노드의 높이를 0이라고 했을 때 트리의 높이가 3인 것을 알 수 있습니다. 따라서 세그먼트 트리의 크기는 2^(트리의 높이 + 1)이 됩니다.
2. 세그먼트 트리 만들기
먼저 주어진 범위를 반으로 나누고, 나누어진 2개의 범위에 대해서 왼쪽과 오른쪽 범위에 대해 각각 재귀호출을 해줍니다. 이를 계속 반복해주다가 리프 노드에 다다르면 재귀를 멈춰주시면 됩니다.
이진트리이므로 항상 범위를 반으로 나누면 됩니다. 즉 (현재 노드, 시작 범위, 끝 범위)의 형태로 반복해서 재귀 호출을 해주고 마지막에 시작 범위와 끝 범위가 일치할 때가 리프 노드이므로 값을 넣어주고 그 값을 return 해주면 됩니다.

3. 세그먼트 트리 구간합 구하기
구간합을 구할 때 조건을 나누어 주면 쉽게 구할 수 있습니다.
1. 현재 탐색하는 범위가 찾고자하는 범위와 완전히 겹치는 경우
2. 현재 탐색하는 범위가 찾고자하는 범위와 일부 겹치는 경우
3. 현재 탐색하는 범위가 찾고자하는 범위와 완전히 겹치지 않는 경우
이를 코드로 표현하면 다음과 같습니다.
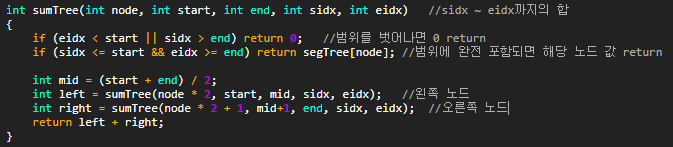
4. 세그먼트 트리 값 바꾸기
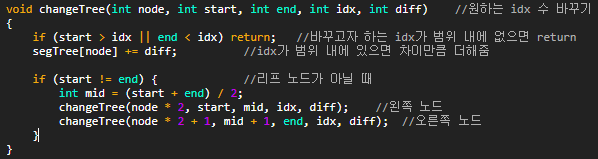
특정 index의 값을 바꿀 때도 분기를 나누어서 구해주면 됩니다. 바꾸고자 하는 index가 현재 범위에 포함되어 있는지 없는지만 체크해주면 쉽게 구현할 수 있습니다.

'자료구조' 카테고리의 다른 글
| [ 자료구조 ] 머지 소트 트리(Merge Sort Tree) (0) | 2023.08.07 |
|---|---|
| [ 자료구조 ] 트라이(Trie) (0) | 2023.06.24 |
| [ 자료구조 ] 비재귀 세그먼트 트리 (Segment Tree) (0) | 2023.05.04 |
| [ 자료구조 ] 느리게 갱신되는 세그먼트 트리 (Lazy Propagation) (0) | 2023.01.16 |
| [ 자료구조 ] 희소 배열(Sparse Table) (0) | 2022.08.07 |