반응형
1. 희소 배열(Sparse Table)
- 배열 원소의 개수가 무조건 배열의 length 값보다 작은 배열
- 희소 배열은 배열의 원소 위치가 연속적이지 않은 배열
2. 희소 배열 만들기
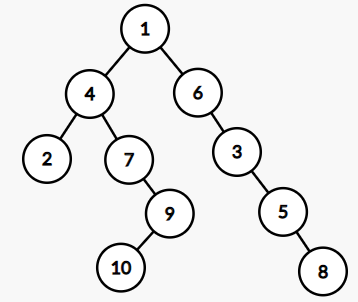
보통 5번 노드에서 1번 노드까지 가기 위해서는 총 3번(5→3→6→1)의 이동이 필요합니다. 하지만 희소 배열로 이동을 한다면 총 2번의 이동이면 충분합니다. (3 = 2 + 1)
이처럼 간선을 1개씩 이동하지 않고, 1, 2, 4, 8... 과 같이 2^i씩 이동한다면 logn번 만에 원하는 노드에 도달할 수 있습니다.
| 이동 횟수 | 1번 이동 | 2번 이동 | 4번 이동 |
| 1 | - | - | - |
| 2 | 4 | 1 | - |
| 3 | 6 | 1 | - |
| 4 | 1 | - | - |
| 5 | 3 | 6 | - |
| 6 | 1 | - | - |
| 7 | 4 | 1 | - |
| 8 | 5 | 3 | 1 |
| 9 | 7 | 4 | - |
| 10 | 9 | 7 | 1 |
[ 소스 코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | // 희소 배열 int sparseTable[n+1][logn+1]; // n은 노드의 번호를, logn은 이동 횟수를 의미 // 희소 배열 생성하여 이동 횟수별 도착 정점 기록 void makeSparseTable() { // 1번 이동해서 도착하는 정점 for (int i=1; i<=n; i++) { sparseTable[i][0] = arr[i]; } // log n번까지 이동해서 도착하는 정점 for (int k=1; k<logn+1; k++) { for (int i=1; i<=n; i++) { int next = sparseTable[i][k-1]; sparseTable[i][k] = sparseTable[next][k-1]; } } } // v 정점에서 출발하여 n개의 간선을 이동하여 도착한 정점 찾기 int find(int n, int v) { for (i=size-1; i>=0; i--) { if ((n & (1<<i))) { v = sparseTable[v][i]; } } } | cs |
반응형
'자료구조' 카테고리의 다른 글
| [ 자료구조 ] 머지 소트 트리(Merge Sort Tree) (0) | 2023.08.07 |
|---|---|
| [ 자료구조 ] 트라이(Trie) (0) | 2023.06.24 |
| [ 자료구조 ] 비재귀 세그먼트 트리 (Segment Tree) (0) | 2023.05.04 |
| [ 자료구조 ] 느리게 갱신되는 세그먼트 트리 (Lazy Propagation) (2) | 2023.01.16 |
| [ 자료구조 ] 세그먼트 트리 (Segment Tree) (0) | 2022.07.02 |