반응형
https://www.acmicpc.net/problem/1086
1086번: 박성원
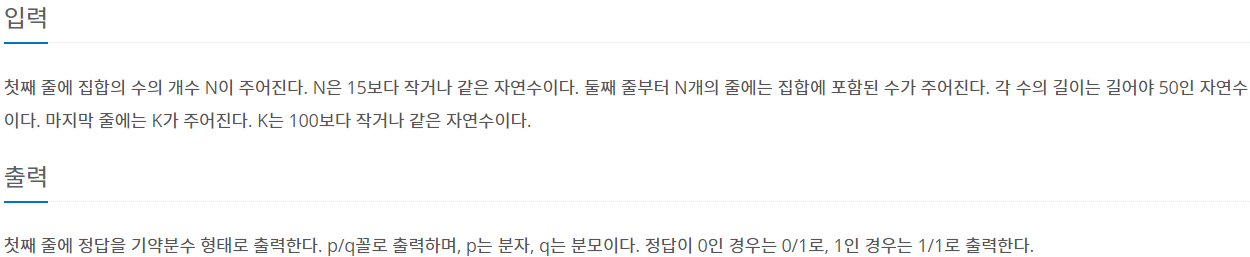
첫째 줄에 정답을 기약분수 형태로 출력한다. p/q꼴로 출력하며, p는 분자, q는 분모이다. 정답이 0인 경우는 0/1로, 1인 경우는 1/1로 출력한다.
www.acmicpc.net
[ 문제풀이 ]
모든 조합에 대해 문제를 푼다면 O(15!)이므로 2초 안에 풀 수 없습니다. 따라서 비트 마스킹을 통해 중복으로 쓰이는 순열들을 저장해서 씀으로써 시간을 줄일 수 있습니다.
또한 $123456$의 나머지를 구할 때는 (123*1000) + 456 이므로 ( ( 123 % K ) * ( 1000 % K ) ) % K + 456 % K로 구해주시면 됩니다.
[ 소스 코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 | #include<iostream> #include<string> #include<cstring> #define ll long long using namespace std; int N, K; string arr[16]; ll dp[1 << 15][100]; int mods[15]; int digit[51]; ll GCD(ll a, ll b) //최대 공약수 구하기 { while (a != 0) { ll temp = b % a; b = a; a = temp; } return b; } int mod(string num) //입력된 숫자를 K로 나눈 나머지 구하기 { int ret = 0; for (int i = 0; i < num.size(); i++) { ret = (ret * 10) % K + (num[i] - '0') % K; ret %= K; } return ret; } ll Fac(int num) //팩토리얼 { ll ret = 1; for (int i = 1; i <= num; i++) { ret *= i; } return ret; } ll DP(int cur, int mod) //나머지별로 개수 저장 { if (cur == (1 << N) - 1) { //모든 수를 썼는가? if (mod == 0) return 1; else return 0; } ll& ret = dp[cur][mod]; if (ret != -1) return dp[cur][mod]; //사용된 적이 있는가? ret = 0; for (int i = 0; i < N; i++) { int mask = 1 << i; if (cur & mask) continue; //이미 사용된 숫자면 continue ret += DP(cur | mask, ((mod * digit[arr[i].size()]) % K + mods[i]) % K); } return ret; } int main() { memset(dp, -1, sizeof(dp)); digit[0] = 1; cin >> N; for (int i = 0; i < N; i++) { cin >> arr[i]; } cin >> K; for (int i = 0; i < N; i++) { mods[i] = mod(arr[i]); } for (int i = 1; i <= 50; i++) { digit[i] = ((digit[i - 1] % K) * (10 % K)) % K; } ll numerator = DP(0, 0); //분자 ll denominator = Fac(N); //분모 if (numerator == 0) { cout << "0/1"; return 0; } if (numerator == denominator) { cout << "1/1"; return 0; } ll gcd = GCD(numerator, denominator); cout << numerator / gcd << "/" << denominator / gcd; } | cs |
반응형
'백준' 카테고리의 다른 글
| [ 백준 ] 1761번 - 정점들의 거리 (C++) (0) | 2022.07.18 |
|---|---|
| [ 백준 ] 1708번 - 볼록 껍질 (C++) (0) | 2022.07.17 |
| [ 백준 ] 17371번 - 이사 (C++) (0) | 2022.07.14 |
| [ 백준 ] 14428번 - 수열과 쿼리 16 (C++) (0) | 2022.07.13 |
| [ 백준 ] 13977번 - 이항 계수와 쿼리 (C++) (0) | 2022.07.12 |