KMP 알고리즘은 문자열을 탐색하는 알고리즘입니다. 보통 ctrl + f를 이용하여 원하는 문자열을 찾을 때 많이 쓰는 방식입니다.
단순하게 길이가 N인 문자열의 처음부터 끝까지 문자열의 길이가 M인 문자열과 비교한다면 O(NM)의 시간이 걸립니다. 하지만 KMP알고리즘을 쓴다면 O(N + M)의 시간으로 문제를 풀 수 있습니다.
[ 동작 원리 ]
먼저 찾고자 하는 문자열 P에 전처리를 해주어야 합니다.
문자열 ABABABAC의 전처리를 예로 들어보겠습니다.

idx가 1일 때 겹치는 문자열의 최대 개수는 0개입니다.

idx가 2일 때 겹치는 문자열의 최대 개수는 1개입니다.
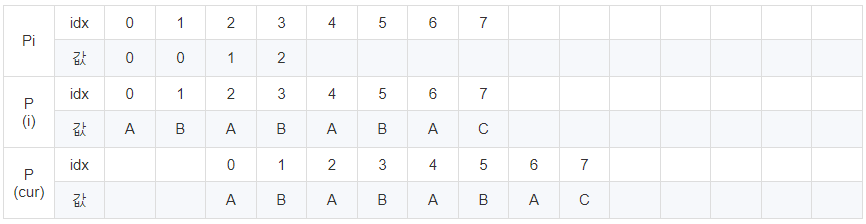
idx가 3일 때 겹치는 문자열의 최대 개수는 2개입니다.

위 방법을 계속 반복하면 위와 같은 결과가 나옵니다.

하지만 idx가 7일 때 문자열이 일치하지 않으므로 cur의 값을 당겨줄 필요가 있습니다.

cur = Pi [cur-1]을 대입해서 Pi[ 5 - 1 ]은 3이므로 위와 같이 당겨줄 수 있습니다.

위와 같은 방법으로 계속 반복면 위와 같은 결과를 얻을 수 있습니다.
이렇게 Pi를 완성시켰습니다.
이제는 이 Pi를 활용해서 KMP를 구해주면 됩니다.

cur이 8일 때 문자열이 다릅니다. 이때 Pi[7] = 6이므로 cur에 6을 대입 후 반복해줍니다.

cur이 6일 때 문자열이 다릅니다. 이 때 Pi [5] = 4이므로 cur에 4를 대입 후 반복해줍니다.

위와 같이 반복하다 보면 일치하는 문자열을 발견할 수 있습니다. 이때 cur은 P.size()-1의 값을 가지고, Pi [cur]은 0이므로 다음 문자열부터 다시 검색을 시작해주면 됩니다.
위 알고리즘을 이용하여 다음 문제를 풀 수 있습니다.
https://rudalsd.tistory.com/70
'알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] 강한 연결 요소 추출 알고리즘(Strongly Connected Component) (0) | 2022.07.23 |
|---|---|
| [ 알고리즘 ] 위상 정렬 알고리즘(Topological Sort Algorithm) (0) | 2022.07.19 |
| [ 알고리즘 ] 컨벡스 헐 알고리즘(Convex Hull Algorithm) (0) | 2022.07.16 |
| [ 알고리즘 ] 페르마의 소정리(Fermat's little theorem) (0) | 2022.07.10 |
| [ 알고리즘 ] 오일러 피 함수(Euler's phi function) (0) | 2022.07.09 |