1. 강한 연결 요소 추출 알고리즘(Strongly Connected Component)이란?
방향성이 존재하는 그래프에서 모든 정점이 다른 모든 정점들에 대하여 방문할 수 있는 경우 즉, 그 부분집합에 들어있는 서로 다른 임의의 두 정점 u, v에 대해서 u에서 v로 가는 경로와 v에서 u로 가는 경로가 모두 존재하는 경우를 말합니다.
2. 강한 연결 요소 추출 알고리즘(Strongly Connected Component)동작 원리?
dfs를 활용하여 O(V+E)의 시간복잡도로 문제를 해결할 수 있습니다. 코사라주 알고리즘과 타잔 알고리즘이 있지만 그 중 더 빠른 타잔 알고리즘을 통해 SCC를 찾겠습니다.
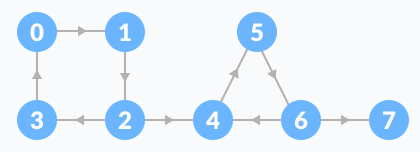
위 그래프의 방문 순서에 따라 id값을 매깁니다. id값은 0부터 시작하며 1씩 증가합니다. 방문 순서는 0→1→2→3→4→5→6→7이 되며 방문할 때마다 해당 정점을 스택에 집어 넣습니다.
각 정점에 대하여 dfs를 수행하여 SCC를 추출해보겠습니다. SCC의 발견 조건은 '자신의 자식 노드(id값이 상대적으로 높을 때)들이 본인의 부모 노드(id값이 상대적으로 낮을 때)로 갈 수 있는 경우의 수가 없는 경우' 이며 이때 스택에서 본인보다 위에 있는 모든 노드들을 빼주고 scc에 넣어주면 됩니다.
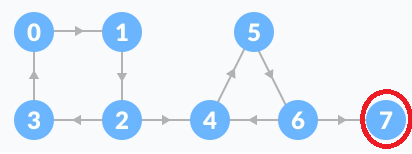

7번 노드는 돌아갈 수 있는 부모 노드가 없으므로 SCC 발견 조건을 만족합니다. 따라서 stack에서 본인이 나올 때까지 숫자를 뽑습니다. stack의 top이 현재 7이므로 7만 빼서 ans에 넣고 계속 진행합니다.
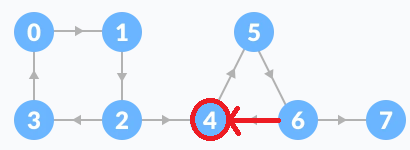

다시 6번 노드에서 4번 노드로 가면 4번 노드는 더 이상 부모 노드로 갈 수 없습니다. 따라서 stack에서 4가 나올 때까지 숫자를 뽑아줍니다.
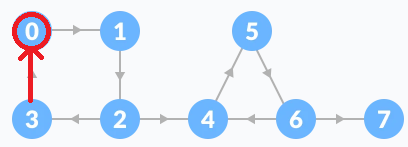

마지막으로 3번 노드에서 0번 노드로 가고 0번 노드는 더이상 부모 노드가 없기 때문에 stack에서 0이 나올 때까지 숫자를 뽑아줍니다.
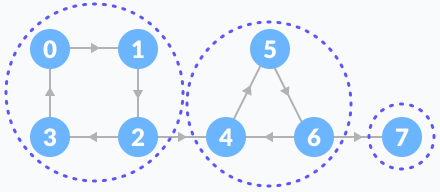

모든 SCC를 발견해서 스택이 비었고, 결과적으로 3개의 SCC가 나옵니다.
이 알고리즘을 이용하여 다음 문제를 풀 수 있습니다.
https://rudalsd.tistory.com/75
'알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] 단절선(Articulation Bridge) (0) | 2022.08.28 |
|---|---|
| [ 알고리즘 ] 단절점(Articulation Point) (0) | 2022.08.26 |
| [ 알고리즘 ] 위상 정렬 알고리즘(Topological Sort Algorithm) (0) | 2022.07.19 |
| [ 알고리즘 ] KMP 알고리즘(KMP Algorithm) (0) | 2022.07.19 |
| [ 알고리즘 ] 컨벡스 헐 알고리즘(Convex Hull Algorithm) (0) | 2022.07.16 |