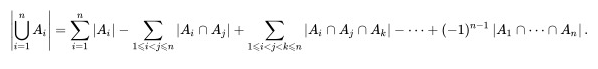https://www.acmicpc.net/problem/17436
17436번: 소수의 배수
첫째 줄에 N(1 ≤ N ≤ 10)과 M(1 ≤ M ≤ 1012)이 주어진다. 둘째 줄에는 N개의 소수가 주어진다. 입력으로 주어지는 소수는 100보다 작거나 같으며, 같은 소수가 두 번 이상 주어지지 않는다.
www.acmicpc.net

[ 문제풀이 ]
이 문제에서는 포함 배제의 원리를 활용해 문제를 풀어야 하므로 다음 글을 일고 오시면 좋습니다!
https://rudalsd.tistory.com/47?category=1064608
[ 알고리즘 ] 포함 배제의 원리(Inclusion–exclusion principle)
오늘은 포함 배제의 원리(Inclusion-exclusion principle)에 대해 설명드리겠습니다. 유한한 집합의 합집합의 총 원소의 개수를 세는 방법입니다. [ 동작 원리 ] 즉, 겹치는 집합의 개수가 홀수이면 해당
rudalsd.tistory.com
N의 최댓값이 10이므로 모든 경우의 수를 생각해도 O(2^10)이므로 0.25초 안에 충분히 풀 수 있습니다.
배열에 소수들을 저장하고, 각 조합의 소수들을 모두 곱한 값으로 M을 나누어 준 몫을 답에 더해주거나 빼주면 됩니다. M보다 작은 값들 중 나누어 떨어지는 수가 몫의 개수만큼 있다는 뜻이기 때문입니다. 만약 조합의 개수가 홀수라면 더해주고, 짝수라면 빼주면 됩니다.
[ 소스 코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | #include<iostream> #include<vector> using namespace std; int N; long long M; int arr[10]; int main() { cin >> N >> M; for (int i = 0; i < N; i++) { cin >> arr[i]; } long long ans = 0; for (int i = 1; i < (1 << N); i++) { int cnt = 0; long long num = 1; for (int j = 0; j < N; j++) { if (i & (1 << j)) { cnt++; //몇 개의 소수가 곱해져 있는지 num *= arr[j]; //소수들을 곱함 } } if (cnt % 2 == 1) { ans += M / num; //M을 소수들을 모두 곱한 값으로 나눈 값을 더함 } else { ans -= M / num; //M을 소수들을 모두 곱한 값으로 나눈 값을 뺌 } } cout << ans; } | cs |
'백준' 카테고리의 다른 글
| [ 백준 ] 2042번 - 구간 합 구하기 (C++) (0) | 2022.07.04 |
|---|---|
| [ 백준 ] 1019번 - 책 페이지 (C++) (0) | 2022.07.03 |
| [ 백준 ] 16565번 - N포커 (C++) (0) | 2022.07.01 |
| [ 백준 ] 15824번 - 너 봄에는 캡사이신이 맛있단다 (C++) (0) | 2022.06.30 |
| [ 백준 ] 13334번 - 철로 (C++) (0) | 2022.06.29 |