반응형

https://www.acmicpc.net/problem/17371

 

17371번: 이사

$(\frac{2}{3}, \frac{1}{3})$으로 이사를 가면 가장 가까운 편의시설은 (0, 1)으로 거리는 $\frac{2\sqrt{2}}{3}$이고, 가장 먼 편의시설은 (-4, 1) 혹은 (4, -3)으로 거리는 둘 다 $\frac{10\sqrt{2}}{3}$이다. 두 거리의

www.acmicpc.net

 

 

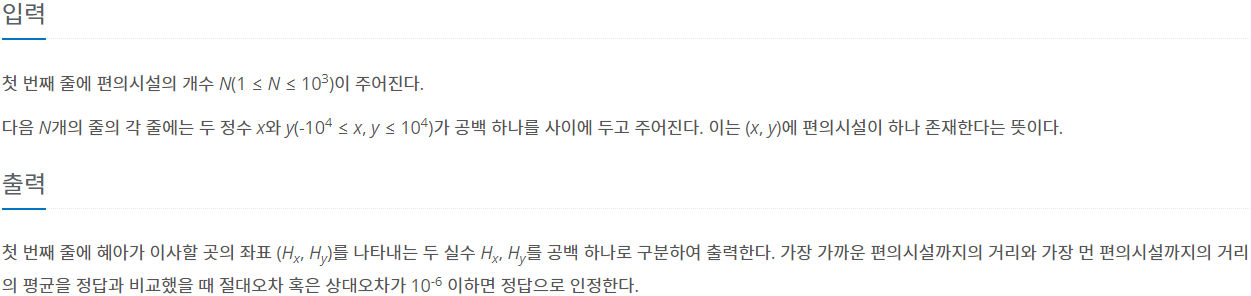
[ 문제풀이 ]

 

생각을 조금만 해보면 쉽게 풀 수 있는 문제입니다.

 

점들 중 하나를 골라 다른 점들과 거리를 비교했을 때 가장 가까운 점은 거리가 0, 가장 먼 거리가 d일 때 평균 거리는 $ \frac{d}{2}$입니다. 따라서 이들 중 가장 짧은 거리를 구해주면 됩니다.

 

[ 소스 코드 ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<iostream>
#include<cmath>
 
using namespace std;
 
int N;
 
struct pos {
    int x;
    int y;
};
 
pos arr[1000];
int ans;
 
int main()
{
    cin >> N;
 
    for (int i = 0; i < N; i++) {
        cin >> arr[i].x >> arr[i].y;
    }
 
    double minDist = 9999999;
 
    for (int i = 0; i < N; i++) {
        int x = 0; int y = 0;
        double maxDist = 0;
        for (int j = 0; j < N; j++) {    //i번째 점부터 j번째 점까지 거리 중 가장 먼 거리를 maxDist에 저장
            double dist = sqrt(pow(arr[i].x - arr[j].x, 2) + pow(arr[i].y - arr[j].y, 2));
            maxDist = max(maxDist, dist);
        }
        
        if (minDist > maxDist) {        //maxDist 중 가장 짧은 거리를 minDist에 저장하고 idx를 ans에 저장
            ans = i;
            minDist = maxDist;
        }
    }
 
    cout << arr[ans].x << " " << arr[ans].y;
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 1708번 - 볼록 껍질 (C++)  (0) 2022.07.17
[ 백준 ] 1086번 - 박성원 (C++)  (0) 2022.07.15
[ 백준 ] 14428번 - 수열과 쿼리 16 (C++)  (0) 2022.07.13
[ 백준 ] 13977번 - 이항 계수와 쿼리 (C++)  (0) 2022.07.12
[ 백준 ] 11689번 - GCD(n, k) = 1 (C++)  (0) 2022.07.11

+ Recent posts

티스토리툴바