https://www.acmicpc.net/problem/16975
16975번: 수열과 쿼리 21
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. 1 i j k: Ai, Ai+1, ..., Aj에 k를 더한다. 2 x: Ax 를 출력한다.
www.acmicpc.net

[ 문제풀이 ]
이 문제를 풀기 전에 다음 글을 먼저 읽고 오시는 것을 추천드립니다.
https://rudalsd.tistory.com/256
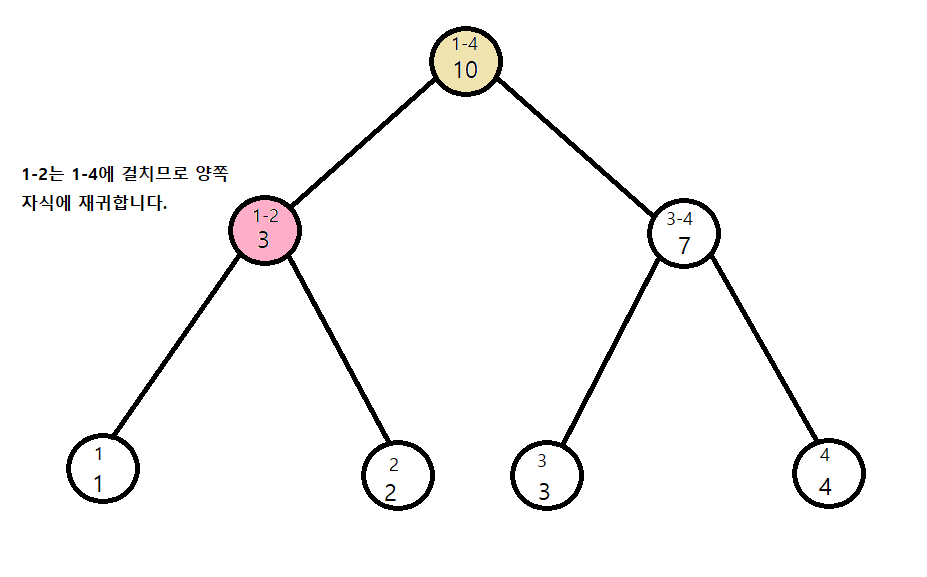
[ 자료구조 ] 느리게 갱신되는 세그먼트 트리 (Lazy Propagation)
https://rudalsd.tistory.com/51 [ 자료구조 ] 세그먼트 트리 (Segment Tree) 1. 세그먼트 트리 (Segment Tree) 먼저, 세그먼트 트리가 무엇인지 알아봅시다! 세그먼트 트리는 구간 합을 저장하기 위한 트리입니다.
rudalsd.tistory.com
1. 세그먼트 트리와 lazy값을 저장할 배열을 만듭니다.
2. 느리게 갱신되는 세그먼트 트리를 활용하여 Update를 하고 원하는 인덱스의 값을 출력합니다.
[ 소스코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 | #include<iostream> #define ll long long using namespace std; int N, M; ll arr[100001]; ll segTree[263000]; ll lazy[263000]; void makeTree(int node, int start, int end) { if (start == end) { segTree[node] = arr[start]; return; } int mid = (start + end) / 2; makeTree(node * 2, start, mid); makeTree(node * 2 + 1, mid + 1, end); segTree[node] = segTree[node * 2] + segTree[node * 2 + 1]; } void modifyLazy(int node, int start, int end) { if (lazy[node] != 0) { segTree[node] += (ll)(end - start + 1) * lazy[node]; if (start != end) { lazy[node * 2] += lazy[node]; lazy[node * 2 + 1] += lazy[node]; } lazy[node] = 0; } } void modifyTree(int node, int start, int end, int i, int j, ll k) { modifyLazy(node, start, end); if (start > j || end < i) return; if (i <= start && end <= j) { lazy[node] += k; modifyLazy(node, start, end); return; } int mid = (start + end) / 2; modifyTree(node * 2, start, mid, i, j, k); modifyTree(node * 2 + 1, mid + 1, end, i, j, k); segTree[node] = segTree[node * 2] + segTree[node * 2 + 1]; } void getTree(int node, int start, int end, int x) { modifyLazy(node, start, end); if (start > x || x > end) return; if (start == end) { arr[start] = segTree[node]; return; } int mid = (start + end) / 2; getTree(node * 2, start, mid, x); getTree(node * 2 + 1, mid + 1, end, x); } int main() { scanf("%d", &N); for (int i = 1; i <= N; i++) { scanf("%lld", &arr[i]); } makeTree(1, 1, N); scanf("%d", &M); for (int m = 0; m < M; m++) { int cmd; scanf("%d", &cmd); if (cmd == 1) { int i, j; ll k; scanf("%d %d %lld", &i, &j, &k); modifyTree(1, 1, N, i, j, k); } else { int x; scanf("%d", &x); getTree(1, 1, N, x); printf("%lld\n", arr[x]); } } } | cs |
'백준' 카테고리의 다른 글
| [ 백준 ] 1777번 - 순열복원 (C++) (0) | 2023.01.20 |
|---|---|
| [ 백준 ] 1849번 - 순열 (C++) (0) | 2023.01.19 |
| [ 백준 ] 10999번 - 구간 합 구하기 2 (C++) (0) | 2023.01.17 |
| [ 백준 ] 5676번 - 음주 코딩 (C++) (0) | 2023.01.15 |
| [ 백준 ] 18436번 - 수열과 쿼리 37 (C++) (0) | 2023.01.14 |