반응형
1. 이분 매칭(Bipartite Matching)이란?
정점을 두 개의 그룹으로 나누었을 때, 존재하는 모든 간선의 양 끝 정점이 서로 다른 그룹에 속하는 형태의 그래프를 이분 그래프(Bipartite Graph)라고 말합니다. 이러한 이분 그래프에서 예를 들어, 한쪽 그룹은 X 그룹, 다른 한쪽 그룹은 Y 그룹이라고 할 때 모든 경로의 방향이 X->Y인 그래프의 최대 유량을 구하는 것이 이분 매칭(Bipartite Matching)입니다.
2. 이분 매칭(Bipartite Matching)동작 원리
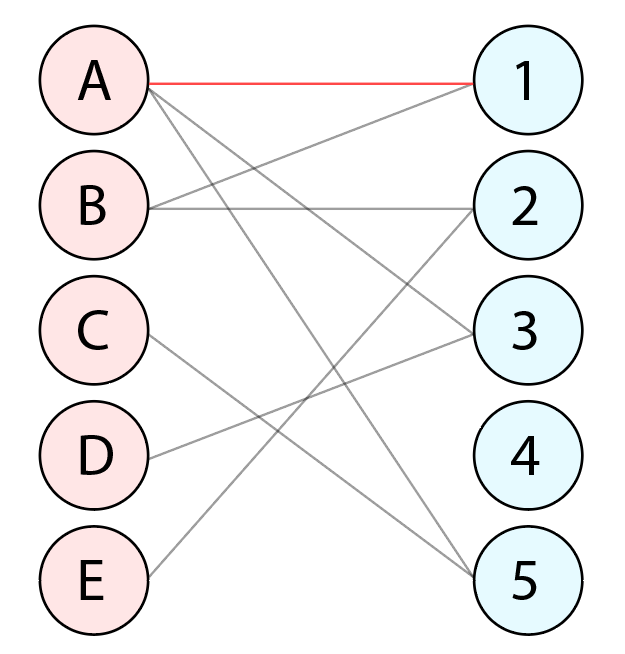
우선, 정점 A는 정점 1을 점유할 수 있습니다. (총 매칭 수 : 1)
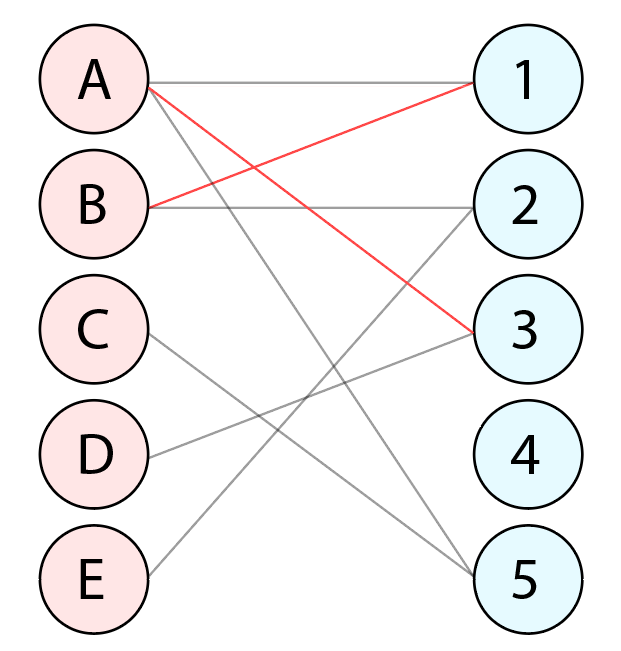
그 다음 정점 B는 정점 1을 점유하려고 합니다. 그런데 정점 A가 이미 정점 1을 보유하고 있으므로 A는 다른 정점을 점유하러 경로를 다시 찾습니다. 정점 3이 비어있으므로 A는 정점 3을 점유합니다. (총 매칭 수 : 2)
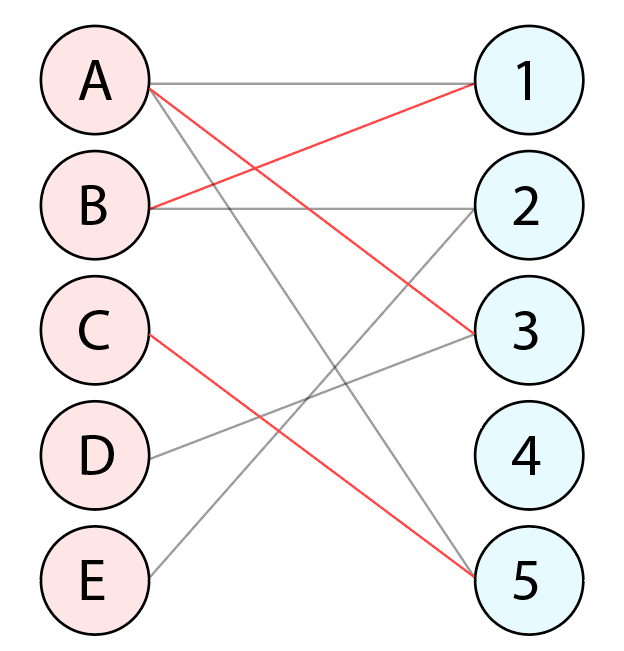
정점 C는 정점 5를 점유합니다. (총 매칭 수 : 3)
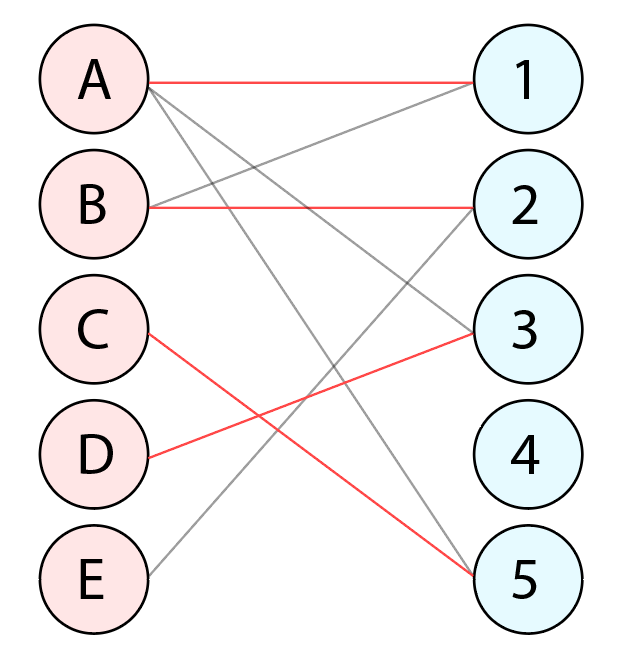
정점 D는 정점 3을 점유하려고 합니다. 그런데 정점 A가 이미 정점 3을 점유하고 있으므로 A가 다른 경로를 찾아 정점 1의 점유를 시도합니다. 그런데 정점 1 역시 정점 B가 점유하고 있으므로 B는 다른 경로를 찾아 비어있던 정점 2를 점유합니다. (총 매칭 수 : 4)
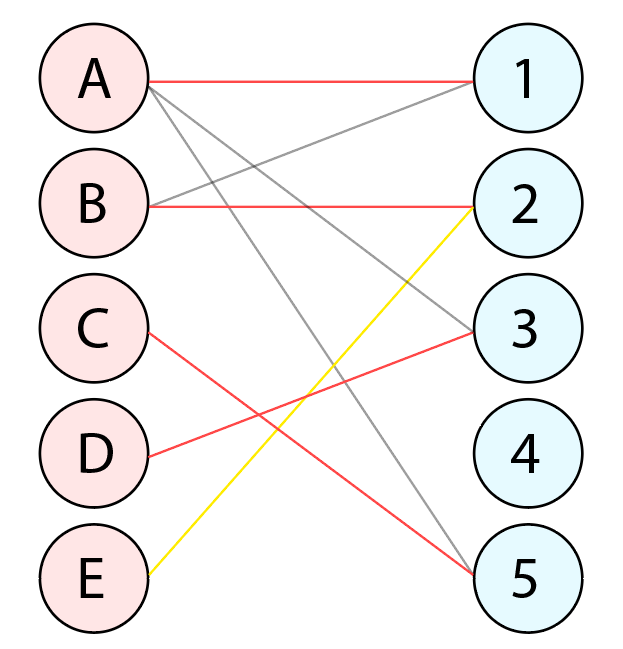
정점 E가 정점 2를 점유하려고 합니다. 그러나 정점 E는 더이상 매칭할 수 없습니다. 2를 점유하면 B가 경로를 다시 찾을 것이고 또 A가 다시 경로를 찾게되며 또 D가 다시 경로를 찾고 계속해서 반복되기 때문에 매칭이 불가능합니다.
따라서 최종 매칭 수는 4가 됩니다.
반응형
'알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] 뤼카의 정리 (Lucas' theorem) (0) | 2023.07.03 |
|---|---|
| [ 알고리즘 ] 최장 증가 부분 수열(Longest Increasing Subsequence) (0) | 2022.10.24 |
| [ 알고리즘 ] 단절선(Articulation Bridge) (0) | 2022.08.28 |
| [ 알고리즘 ] 단절점(Articulation Point) (0) | 2022.08.26 |
| [ 알고리즘 ] 강한 연결 요소 추출 알고리즘(Strongly Connected Component) (0) | 2022.07.23 |