반응형

https://www.acmicpc.net/problem/1725

 

1725번: 히스토그램

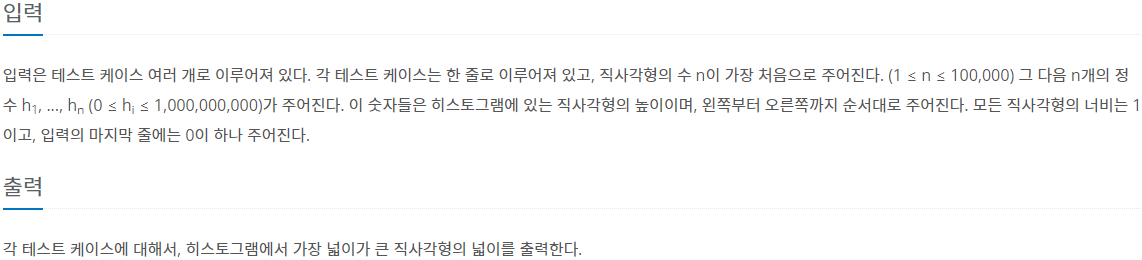
첫 행에는 N (1 ≤ N ≤ 100,000) 이 주어진다. N은 히스토그램의 가로 칸의 수이다. 다음 N 행에 걸쳐 각 칸의 높이가 왼쪽에서부터 차례대로 주어진다. 각 칸의 높이는 1,000,000,000보다 작거나 같은

www.acmicpc.net

 

 

[ 문제풀이 ]

 

다음과 같은 순서대로 문제를 풀어주시면 쉽게 답을 구할 수 있습니다.

 

1. push 하려는 막대의 높이가 s.top() 인덱스의 막대 높이보다 크거나 같다면 계속해서 스택을 쌓습니다. 

 

2. 만약 push 하려는 막대의 높이가 s.top() 인덱스의 막대 높이보다 작다면 s.top()이 push 하려는 막대 높이보다 커질 때까지 s.pop()을 해줍니다.

 

3. s.pop()을 할 때마다 직사각형의 넓이를 구하고 최댓값을 저장합니다.

 

다음 글은 세그먼트 트리와 분할 정복을 통해 문제를 푸는 방법입니다.

https://rudalsd.tistory.com/88?category=1064612 

 

[ 소스 코드 ]

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<stack>
 
using namespace std;
 
int N;
int arr[100005];
int ans;
 
int main()
{
    stack<int> s;
    s.push(0);
    scanf("%d", &N);
 
    for (int i = 1; i <= N; i++) {
        scanf("%d", &arr[i]);
    }
 
    for (int i = 1; i <= N + 1; i++) {
        while (!s.empty() && arr[i] < arr[s.top()]) {
            int cur = s.top();
            s.pop();
            int W = arr[cur] * (i - s.top() - 1);
            ans = max(ans, W);
        }
        s.push(i);
    }
 
    printf("%d", ans);
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 10026번 - 적록색약 (C++)  (0) 2022.08.05
[ 백준 ] 11438번 - LCA 2 (C++)  (0) 2022.08.04
[ 백준 ] 6549번 - 히스토그램에서 가장 큰 직사각형 (C++)  (0) 2022.08.02
[ 백준 ] 1629번 - 곱셈 (C++)  (0) 2022.08.01
[ 백준 ] 11725번 - 트리의 부모 찾기 (C++)  (0) 2022.07.31
반응형

https://www.acmicpc.net/problem/6549

 

6549번: 히스토그램에서 가장 큰 직사각형

입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤

www.acmicpc.net

 

 

[ 문제풀이 ]

 

이 문제를 풀기 전에 다음 글을 먼저 읽고 오시는 것을 추천드립니다!!

https://rudalsd.tistory.com/51?category=1073064 

 

[ 자료구조 ] 세그먼트 트리 (Segment Tree)

1. 세그먼트 트리 (Segment Tree) 먼저, 세그먼트 트리가 무엇인지 알아봅시다! 세그먼트 트리는 구간 합을 저장하기 위한 트리입니다. 예를 들어 size가 5인 배열이 있다고 생각해봅시다. int arr [5] = {1

rudalsd.tistory.com

 

먼저 높이 값이 가장 작은 idx를 각각의 노드에 저장하는 세그먼트 트리를 만듭니다. 그 후 일정 구간에서 가장 작은 높이를 가지는 idx를 구하는 함수를 만든 후 그 idx를 기준으로 왼쪽 오른쪽으로 나누어 분할 정복을 해주시면 됩니다.

 

다음 글은 스택을 활용하여 문제를 푸는 방법입니다.

https://rudalsd.tistory.com/89?category=1064612 

 

[ 소스 코드 ]

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<iostream>
#include<cmath>
 
#define ll long long
 
using namespace std;
 
int n;
int segTree[300000];
ll arr[100001];
ll ans;
 
int makeTree(int node, int start, int end)        //세그먼트 트리 만들기
{
    if (start == end) {        //리프노드
        return segTree[node] = start;
    }
 
    int mid = (start + end) / 2;
    int left = makeTree(node * 2, start, mid);        //왼쪽 자식 노드
    int right = makeTree(node * 2 + 1, mid + 1, end);    //오른쪽 자식 노드
 
    return segTree[node] = arr[left] > arr[right] ? right : left;
}
 
int find(int node, int start, int end, int sidx, int eidx)    //최소 높이의 idx return
{
    if (eidx < start || sidx > end) return 0;    //범위에 완전히 포함되지 않을 때
    if (start >= sidx && end <= eidx) return segTree[node];    //범위에 완전히 포함될 때
    //범위에 일부 포함될 때
    int mid = (start + end) / 2;
    int left = find(node * 2, start, mid, sidx, eidx);
    int right = find(node * 2 + 1, mid + 1, end, sidx, eidx);
 
    if (left == 0) return right;
    if (right == 0) return left;
    return arr[left] > arr[right] ? right : left;
}
 
void getMax(int start, int end)
{
    if (start > end) return;
    int min = find(1, 1, n, start, end);
 
    ll W = arr[min] * (end - start + 1);
    ans = max(ans, W);
 
    getMax(start, min - 1);
    getMax(min + 1, end);
}
 
int main()
{
    while (1)
    {
        ans = 0;
        scanf("%d", &n);
        if (n == 0)break;
        for (int i = 1; i <= n; i++) {
            scanf("%lld", &arr[i]);
        }
 
        makeTree(1, 1, n);
 
        getMax(1, n);
 
        printf("%lld\n", ans);
    }
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 11438번 - LCA 2 (C++)  (0) 2022.08.04
[ 백준 ] 1725번 - 히스토그램 (C++)  (0) 2022.08.03
[ 백준 ] 1629번 - 곱셈 (C++)  (0) 2022.08.01
[ 백준 ] 11725번 - 트리의 부모 찾기 (C++)  (0) 2022.07.31
[ 백준 ] 11444번 - 피보나치 수 6 (C++)  (0) 2022.07.30
반응형

https://www.acmicpc.net/problem/1629

 

1629번: 곱셈

첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.

www.acmicpc.net

 

 

[ 문제풀이 ]

 

가장 기본적인 분할 정복 문제입니다. 제곱수의 값이 짝수이면 제곱수를 반으로 나누어 서로 곱하는 방식으로 진행하여 시간 복잡도를 O(logN)으로 줄일 수 있습니다. 시간을 더 단축하기 위해서 메모제이션을 해주어야 문제를 풀 수 있습니다.

 

[ 소스 코드 ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
#include<unordered_map>
 
#define ll long long
 
using namespace std;
 
ll A, B, C;
unordered_map<ll, ll> m;
 
ll conquer(ll num)
{
    if (num == 0) return 1;
    if (num == 1) return A % C;
    if (m[num] != 0) return m[num] % C;
 
    if (num % 2 == 0) {
        m[num] = conquer(num / 2) * conquer(num / 2);
        return m[num] % C;
    }
    else {
        m[num] = conquer(num - 1) * A;
        return m[num] % C;
    }
}
 
int main()
{
    scanf("%lld %lld %lld", &A, &B, &C);
 
    printf("%lld", conquer(B) % C);
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 1725번 - 히스토그램 (C++)  (0) 2022.08.03
[ 백준 ] 6549번 - 히스토그램에서 가장 큰 직사각형 (C++)  (0) 2022.08.02
[ 백준 ] 11725번 - 트리의 부모 찾기 (C++)  (0) 2022.07.31
[ 백준 ] 11444번 - 피보나치 수 6 (C++)  (0) 2022.07.30
[ 백준 ] 2243번 - 사탕상자 (C++)  (0) 2022.07.29
반응형

https://www.acmicpc.net/problem/11725

 

11725번: 트리의 부모 찾기

루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.

www.acmicpc.net

 

 

[ 문제풀이 ]

 

먼저 vector를 이용하여 그래프 입력을 받고, 입력받은 그래프를 바탕으로 DFS를 돌려 문제를 풀 수 있습니다. 한번 방문한 노드는 다시 방문할 필요가 없으므로 visited배열을 통해 방문 체크를 해주시면 됩니다.

 

[ 소스 코드 ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<iostream>
#include<vector>
 
using namespace std;
 
int N;
vector<int> list[100001];
int visited[100001];
int parent[100001];
 
void dfs(int node)
{
    if (visited[node] == 1) return;
    visited[node] = 1;
 
    for (auto next : list[node]) {
        if (visited[next] != 1) {
            parent[next] = node;
            dfs(next);
        }
    }
}
 
int main()
{
    scanf("%d", &N);
 
    for (int i = 0; i < N - 1; i++) {
        int a, b;
        scanf("%d %d", &a, &b);
        list[a].push_back(b);
        list[b].push_back(a);
    }
 
    dfs(1);
 
    for (int i = 2; i <= N; i++) {
        printf("%d\n", parent[i]);
    }
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 6549번 - 히스토그램에서 가장 큰 직사각형 (C++)  (0) 2022.08.02
[ 백준 ] 1629번 - 곱셈 (C++)  (0) 2022.08.01
[ 백준 ] 11444번 - 피보나치 수 6 (C++)  (0) 2022.07.30
[ 백준 ] 2243번 - 사탕상자 (C++)  (0) 2022.07.29
[ 백준 ] 5719번 - 거의 최단 경로 (C++)  (0) 2022.07.27
반응형

https://www.acmicpc.net/problem/11444

 

11444번: 피보나치 수 6

첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.

www.acmicpc.net

 

 

[ 문제풀이 ]

 

분할 정복과 도가뉴의 방정식을 이용하면 쉽게 풀 수 있는 문제입니다. 또한 시간 초과를 방지하기 위해서 메모제이션을 해주어야 하는데 n의 값이 매우 크므로 unordered_map을 활용하여 문제를 풀었습니다.

 

도가뉴의 방정식은 다음과 같습니다.

 

$a_{2n}=a_{n}(a_{n} + 2a_{n-1})$

$a_{2n-1}=a_{n}^{2}+a_{n-1}^{2}$

 

[ 소스 코드 ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<iostream>
#include<unordered_map>
 
#define ll long long
 
using namespace std;
 
ll n;
unordered_map<ll, ll> m;
 
ll conquer(ll num)
{
    if (num == 1) return 1;
    if (num == 0) return 0;
    if (m[num] != 0) return m[num];
    if (num % 2 == 0) {        //도가뉴의 항등식
        ll temp = num / 2;
        m[num] = conquer(temp)*(conquer(temp) + 2 * conquer(temp - 1));
        return m[num] %= 1000000007;
    }
    else {
        ll temp = (num + 1) / 2;
        m[num] = conquer(temp) * conquer(temp) + conquer(temp - 1) * conquer(temp - 1);
        return m[num] %= 1000000007;
    }
}
 
int main()
{
    scanf("%lld", &n);
 
    printf("%lld", conquer(n));
}
cs

 

반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 1629번 - 곱셈 (C++)  (0) 2022.08.01
[ 백준 ] 11725번 - 트리의 부모 찾기 (C++)  (0) 2022.07.31
[ 백준 ] 2243번 - 사탕상자 (C++)  (0) 2022.07.29
[ 백준 ] 5719번 - 거의 최단 경로 (C++)  (0) 2022.07.27
[ 백준 ] 2618번 - 경찰차 (C++)  (0) 2022.07.26
반응형

https://www.acmicpc.net/problem/2243

 

2243번: 사탕상자

첫째 줄에 수정이가 사탕상자에 손을 댄 횟수 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 n개의 줄에는 두 정수 A, B, 혹은 세 정수 A, B, C가 주어진다. A가 1인 경우는 사탕상자에서 사탕을 꺼내는 경우이

www.acmicpc.net

 

 

[ 문제풀이 ]

 

이 문제를 풀기 전에 다음 글을 먼저 읽어보시는 것을 추천드립니다!!

 

https://rudalsd.tistory.com/51?category=1073064 

 

[ 자료구조 ] 세그먼트 트리 (Segment Tree)

1. 세그먼트 트리 (Segment Tree) 먼저, 세그먼트 트리가 무엇인지 알아봅시다! 세그먼트 트리는 구간 합을 저장하기 위한 트리입니다. 예를 들어 size가 5인 배열이 있다고 생각해봅시다. int arr [5] = {1

rudalsd.tistory.com

 

각각의 노드들에는 왼쪽 자식 노드 값 + 오른쪽 자식 노드 값을 넣어줍니다. 노드의 값은 가지고 있는 사탕의 개수이고, 이를 활용해서 특정 idx에 무슨 맛의 사탕이 있는지 알아낼 수 있습니다.

 

오른쪽 노드로 내려갈 때는 오른쪽 노드의 사탕 개수만 가지고 때문에 왼쪽 노드의 사탕 개수는 포함되어 있지 않습니다.

 

따라서, 오른쪽 노드로 내려갈 때는 idx에서 왼쪽 노드의 값을 빼주는 방법을 이용하여 문제를 풀 수 있습니다.

 

[ 소스 코드 ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<iostream>
 
using namespace std;
 
int n;
int segTree[2111111];
 
void update(int node, int start, int end, int taste, int N)    //사탕 숫자 update
{
    if (taste > end || taste < start) return;    //범위를 벗어나면
 
    segTree[node] += N;
 
    if (start == end) return;    //범위에 완전히 포함되면
 
    //범위에 일부 포함되면
    int mid = (start + end) / 2;
    update(node * 2, start, mid, taste, N);
    update(node * 2 + 1, mid + 1, end, taste, N);
}
 
int get(int node, int start, int end, int idx)    //idx번째 사탕의 맛 얻기
{
    if (start == end) {        //범위에 정확히 들어오면
        return start;
    }
 
    int mid = (start + end) / 2;
    if (segTree[node * 2] >= idx) return get(node * 2, start, mid, idx);    //왼쪽 자식 노드
    return get(node * 2 + 1, mid + 1, end, idx - segTree[node * 2]);        //오른쪽 자식 노드
}
 
int main()
{
    scanf("%d", &n);
 
    for (int i = 0; i < n; i++) {
        int A, B, C;
        scanf("%d", &A);
 
        if (A == 1) {        //사탕 꺼내기
            scanf("%d", &B);
            int idx = get(1, 1, 1000000, B);
            printf("%d\n", idx);
            update(1, 1, 1000000, idx, -1);
        }
        else {                //사탕 넣고, 빼기
            scanf("%d %d", &B, &C);
            update(1, 1, 1000000, B, C);
        }
    }
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 11725번 - 트리의 부모 찾기 (C++)  (0) 2022.07.31
[ 백준 ] 11444번 - 피보나치 수 6 (C++)  (0) 2022.07.30
[ 백준 ] 5719번 - 거의 최단 경로 (C++)  (0) 2022.07.27
[ 백준 ] 2618번 - 경찰차 (C++)  (0) 2022.07.26
[ 백준 ] 14938번 - 서강그라운드 (C++)  (0) 2022.07.25
반응형

RaspberryPi 시리얼 통신

serialport install

  • 라즈베리파이에서 시리얼 통신을 하기 위해서는 serialport 모듈을 설치해야합니다.

    npm i serialport

main.js 작성

  • serialport 모듈은 nodejs에서 작동하므로 javascript를 작성해주어야합니다.

    const SerialPort = require("serialport");
const port = new SerialPort({
    path: "/dev/ttyACM0",
    baudRate: 115200,
    dataBits: 8,
    stopBits: 1,
    parity: "none",
});

시리얼 통신 시작

  • 내장된 함수를 이용해서 시리얼 통신을 시작합니다.
    port.write("Hi\n"); //아두이노로 Hi\n라는 문자열을 전송
반응형
저작자표시 비영리 변경금지 (새창열림)

'RaspberryPi' 카테고리의 다른 글

[ RasberryPi ] 라즈베리파이 설정 (Raspi-setup)  (0) 2022.07.22
반응형

https://www.acmicpc.net/problem/5719

 

5719번: 거의 최단 경로

입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 장소의 수 N (2 ≤ N ≤ 500)과 도로의 수 M (1 ≤ M ≤ 104)가 주어진다. 장소는 0부터 N-1번까지 번호가 매겨져 있

www.acmicpc.net

 

 

[ 문제풀이 ]

 

데이크스트라를 이용해 최단거리를 구하고 경로를 저장한 다음 역으로 최단 거리 경로들을 지워준 후 다시 데이크스트라를 이용하여 거의 최단 경로를 구해줍니다.

 

경로를 저장하는 방식은 다음과 같습니다.

 

 

위의 그림을 예로 들면 빨간색 길이 최단경로입니다. 이때 link [7] = {3,5}, link [3] = {2}, link [2] = {1}, link [5] = {1}로 저장합니다.

 

7번 노드부터 역으로 가면서 간선들을 지워주면 거의 최단 경로는 1 -> 4 -> 7이 됩니다.

 

[ 소스 코드 ]

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
 
using namespace std;
 
struct node {
    int to;
    int dist;
};
 
struct cmp {
    bool operator()(node right, node left)
    {
        return left.dist < right.dist;
    }
};
 
int N, M, S, D;
vector<vector<node>> list;        //그래프
vector<vector<int>> link;        //link[i] = {j} j->i까지의 거리가 최단거리
int routed[500][500];            //지울 간선
int dijk[500];            //각 노드까지의 최단 거리
 
 
int dijkstra()        //최단 거리를 구하는 함수
{
    priority_queue<node, vector<node>, cmp> pq;
    pq.push({ S,0 });
 
    for (int i = 0; i < N; i++) {
        dijk[i] = 987654321;
    }
 
    dijk[S] = 0;
 
    while (!pq.empty())
    {
        int cur = pq.top().to;
        int dist = pq.top().dist;
        pq.pop();
 
        if (dijk[cur] < dist) continue;    //최단 거리가 아니라면
 
        for (int i = 0; i < list[cur].size(); i++) {
            int next = list[cur][i].to;
            int nDist = list[cur][i].dist;
 
            if (routed[cur][next] == 1) {    //사라진 간선이라면
                continue;
            }
 
            if (dijk[next] == dist + nDist) {    //최단거리와 같다면
                link[next].push_back(cur);
            }
            else if (dijk[next] > dist + nDist) {    //최단 거리가 갱신된다면
                link[next].clear();
                link[next].push_back(cur);
 
                dijk[next] = dist + nDist;
                pq.push({ next,dist + nDist });
            }
        }
    }
 
    return dijk[D] == 987654321 ? -1 : dijk[D];
}
 
void remove(int cur)
{
    for (int i = 0; i < link[cur].size(); i++) {    //현재 노드에 연결된 최단 거리 노드
        int node = link[cur][i];
        if (routed[node][cur] != 1) {
            routed[node][cur] = 1;        //경로에서 제거
 
            remove(node);            //연결된 노드에 또 연결된 최단 거리 노드들 제거
        }
    }
}
 
int main()
{
    while (1) {
        scanf("%d %d", &N, &M);
        memset(routed, 0, sizeof(routed));
 
        list.clear();
        list.resize(N);
        link.clear();
        link.resize(N);
 
        if (N == 0) {
            break;
        }
 
        scanf("%d %d", &S, &D);
 
        for (int i = 0; i < M; i++) {
            int U, V, P;
            scanf("%d %d %d", &U, &V, &P);
            list[U].push_back({ V,P });
        }
 
        dijkstra();
        remove(D);
        printf("%d\n", dijkstra());
    }
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 11444번 - 피보나치 수 6 (C++)  (0) 2022.07.30
[ 백준 ] 2243번 - 사탕상자 (C++)  (0) 2022.07.29
[ 백준 ] 2618번 - 경찰차 (C++)  (0) 2022.07.26
[ 백준 ] 14938번 - 서강그라운드 (C++)  (0) 2022.07.25
[ 백준 ] 2150번 - Strongly Connected Component (C++)  (0) 2022.07.24
반응형

https://www.acmicpc.net/problem/2618

 

2618번: 경찰차

첫째 줄에는 동서방향 도로의 개수를 나타내는 정수 N(5 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 처리해야 하는 사건의 개수를 나타내는 정수 W(1 ≤ W ≤ 1,000)가 주어진다. 셋째 줄부터 (W+2)번째 줄

www.acmicpc.net

 

 

[ 문제풀이 ]

 

재귀 함수와 다이나믹 프로그래밍으로 풀 수 있는 문제입니다.

 

먼저 dp[dp [ 1001 ][ 1001 ] 배열을 만듭니다. dp [ a ][ b ]에서 a는 1번 자동차의 위치, b는 2번 자동차의 위치입니다. 더 정확하게는 a번째 사건의 위치가 현재 1번 자동차의 위치, b번째 사건의 위치가 현재 2번 자동차의 위치입니다.

 

dist1은 현재 1번 자동차의 위치에서 다음 사건 위치로 옮길 때의 거리, dist2는 현재 2번 자동차의 위치에서 다음 사건 위치로 옮길 때의 거리입니다.

 

[ 소스 코드 ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include<iostream>
#include<cmath>
 
using namespace std;
 
struct acc {        //사고의 위치 struct
    int y;
    int x;
};
 
int N, W;
 
acc arr[1001];        //사고의 위치를 저장할 배열
int dp[1001][1001];    //dp[a][b] a는 1번 자동차, b는 2번 자동차의 현재 사건 위치
 
int dist(acc a, acc b)        //a점과 b점의 거리 return
{
    return abs(a.x - b.x) + abs(a.y - b.y);
}
 
int dfs(int a, int b)
{
    if (a == W || b == W) return 0;    //마지막 사건이라면
    if (dp[a][b] != 0) return dp[a][b];    //한번이라도 저장되었다면
 
    int nAcc = max(a, b) + 1;    //다음 사고 번호
    int dist1, dist2;
 
    if (a == 0) {        //1번 자동차가 움직였을 때의 거리
        dist1 = dist(arr[nAcc], { 1,1 });
    }
    else {
        dist1 = dist(arr[nAcc], arr[a]);
    }
    if (b == 0) {        //2번 자동차가 움직였을 때의 거리
        dist2 = dist(arr[nAcc], { N,N });
    }
    else {
        dist2 = dist(arr[nAcc], arr[b]);
    }
 
    return dp[a][b] = min(dist1 + dfs(nAcc, b), dist2 + dfs(a, nAcc));
}
 
void route(int a, int b)
{
    if (a == W || b == W) return;
 
    int nAcc = max(a, b) + 1;
    int dist1, dist2;
 
    if (a == 0) {
        dist1 = dist(arr[nAcc], { 1,1 });
    }
    else {
        dist1 = dist(arr[nAcc], arr[a]);
    }
    if (b == 0) {
        dist2 = dist(arr[nAcc], { N,N });
    }
    else {
        dist2 = dist(arr[nAcc], arr[b]);
    }
 
    if (dp[nAcc][b] + dist1 < dp[a][nAcc] + dist2) {
        printf("1\n");        //1번 자동차가 움직이는 게 가장 짧은 거리일 때
        route(nAcc, b);
    }
    else {                    //2번 자동차가 움직이는 게 가장 짧은 거리일 때
        printf("2\n");
        route(a, nAcc);
    }
 
}
 
int main()
{
    cin >> N >> W;
 
    for (int i = 1; i <= W; i++) {
        scanf("%d %d", &arr[i].y, &arr[i].x);
    }
 
    printf("%d\n", dfs(0, 0));
    route(0, 0);
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 2243번 - 사탕상자 (C++)  (0) 2022.07.29
[ 백준 ] 5719번 - 거의 최단 경로 (C++)  (0) 2022.07.27
[ 백준 ] 14938번 - 서강그라운드 (C++)  (0) 2022.07.25
[ 백준 ] 2150번 - Strongly Connected Component (C++)  (0) 2022.07.24
[ 백준 ] 1948번 - 임계경로 (C++)  (0) 2022.07.22
반응형

https://www.acmicpc.net/problem/14938

 

14938번: 서강그라운드

예은이는 요즘 가장 인기가 있는 게임 서강그라운드를 즐기고 있다. 서강그라운드는 여러 지역중 하나의 지역에 낙하산을 타고 낙하하여, 그 지역에 떨어져 있는 아이템들을 이용해 서바이벌을

www.acmicpc.net

 

 

[ 문제풀이 ]

 

데이크스트라를 이용하여 쉽게 풀 수 있는 문제입니다.

 

낙하 지역을 1부터 n까지 다 돌면서 데이크스트라를 적용시켜주면 됩니다. 거리 내에 있는 지역들을 들르면서 아이템의 개수를 더해주고, 거리를 벗어나면 continue 해주는 방법으로 문제를 풀었습니다.

 

[ 소스 코드 ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<iostream>
#include<vector>
#include<queue>
 
using namespace std;
 
struct node {        //노드의 정보를 저장할 struct
    int to;            //다음 노드
    int dist;        //다음 노드까지의 거리
};
 
struct cmp {        //priority_queue 비교 연산자
    bool operator()(node right, node left)
    {
        return left.dist < right.dist;
    }
};
 
int n, m, r;
int item[101];        //각 지역의 아이템 수를 저장할 배열
vector<node> list[101];    //그래프
 
int main()
{
    cin >> n >> m >> r;
 
    for (int i = 1; i <= n; i++) {
        cin >> item[i];
    }
 
    for (int i = 0; i < r; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        list[a].push_back({ b,c });
        list[b].push_back({ a,c });
    }
 
    int ans = 0;
 
    for (int i = 1; i <= n; i++) {    //모든 지역 탐색
        int cnt = 0;
        priority_queue < node, vector<node>, cmp> pq;
        int visited[101] = { 0 };
 
        pq.push({ i, 0 });
 
        while (!pq.empty())
        {
            int to = pq.top().to;
            int dist = pq.top().dist;
            pq.pop();
 
            if (visited[to] == 1 || dist > m) continue;    //방문했거나 거리가 멀면 continue
            visited[to] = 1;
            cnt += item[to];
 
            for (int i = 0; i < list[to].size(); i++) {
                int next = list[to][i].to;
                int nDist = list[to][i].dist;
                if (visited[next] == 0) {
                    pq.push({ next, nDist + dist });
                }
            }
        }
 
        if (ans < cnt) {
            ans = cnt;
        }
    }
 
    cout << ans;
}
cs
반응형
저작자표시 비영리 변경금지 (새창열림)

'백준' 카테고리의 다른 글

[ 백준 ] 5719번 - 거의 최단 경로 (C++)  (0) 2022.07.27
[ 백준 ] 2618번 - 경찰차 (C++)  (0) 2022.07.26
[ 백준 ] 2150번 - Strongly Connected Component (C++)  (0) 2022.07.24
[ 백준 ] 1948번 - 임계경로 (C++)  (0) 2022.07.22
[ 백준 ] 10830번 - 행렬 제곱 (C++)  (0) 2022.07.21

+ Recent posts

티스토리툴바