https://www.acmicpc.net/problem/11376
11376번: 열혈강호 2
강호네 회사에는 직원이 N명이 있고, 해야할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다. 각 직원은 최대 두 개의 일을 할 수 있고,
www.acmicpc.net

[ 문제풀이 ]
이 문제를 풀기 전에 다음 글을 먼저 읽고 오시는 것을 추천드립니다.
https://rudalsd.tistory.com/384
[ 알고리즘 ] 이분 매칭(Bipartite Matching)
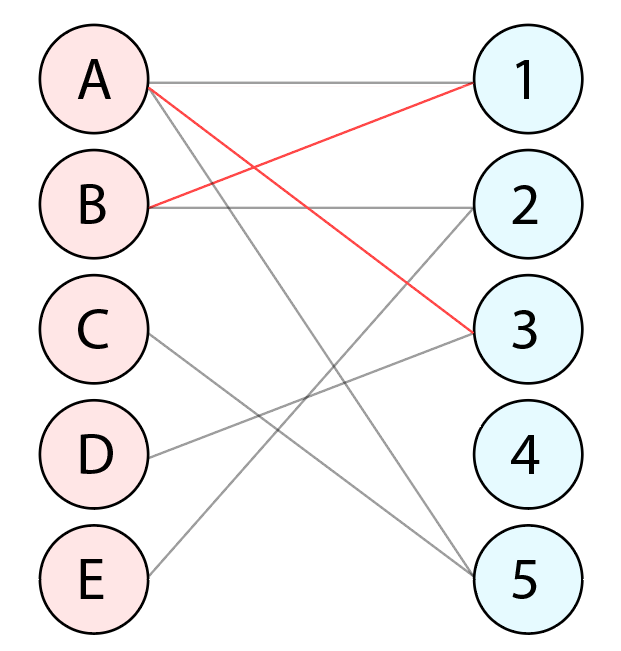
1. 이분 매칭(Bipartite Matching)이란? 정점을 두 개의 그룹으로 나누었을 때, 존재하는 모든 간선의 양 끝 정점이 서로 다른 그룹에 속하는 형태의 그래프를 이분 그래프(Bipartite Graph)라고 말합니다.
rudalsd.tistory.com
1. 한 명이 총 2개의 일을 할 수 있으므로 N * 2의 범위까지 사람을 늘리고, i * 2 와 i * 2 - 1 을 한 사람으로 생각하고 문제를 풉니다.
2. 이분 매칭을 이용하여 매칭이 될 때마다 ans에 1을 더해줍니다.
3. ans를 출력합니다.
[ 소스코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | #include<iostream> #include<vector> using namespace std; int N, M; vector<int> list[2001]; int visited[2001]; int work[1001]; int cnt; bool dfs(int cur) { if (visited[cur] == cnt) return false; visited[cur] = cnt; for (int& next : list[cur]) { if (!work[next] || dfs(work[next])) { work[next] = cur; return true; } } return false; } int main() { scanf("%d %d", &N, &M); for (int i = 1; i <= N; i++) { int n; scanf("%d", &n); for (int j = 0; j < n; j++) { int m; scanf("%d", &m); list[i * 2].push_back(m); list[i * 2 - 1].push_back(m); } } int ans = 0; for (int i = 1; i <= N * 2; i++) { cnt++; if(dfs(i)) ans++; } printf("%d", ans); } | cs |
'백준' 카테고리의 다른 글
| [ 백준 ] 12899번 - 데이터 구조 (C++) (0) | 2023.05.28 |
|---|---|
| [ 백준 ] 18116번 - 로봇 조립 (C++) (0) | 2023.05.27 |
| [ 백준 ] 11375번 - 열혈강호 (C++) (0) | 2023.05.25 |
| [ 백준 ] 2934번 - LRH 식물 (C++) (0) | 2023.05.23 |
| [ 백준 ] 14245번 - XOR (C++) (0) | 2023.05.22 |