https://www.acmicpc.net/problem/2150
2150번: Strongly Connected Component
첫째 줄에 두 정수 V(1 ≤ V ≤ 10,000), E(1 ≤ E ≤ 100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정
www.acmicpc.net

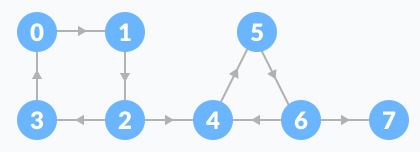
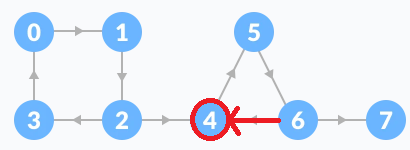
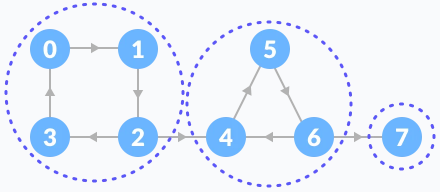
[ 문제풀이 ]
이 문제를 풀기 전에 다음 글을 먼저 읽고 오시는 것을 추천드립니다!!
https://rudalsd.tistory.com/74?category=1064608
[ 소스 코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 | #include<iostream> #include<stack> #include<vector> #include<algorithm> using namespace std; int V, E; vector<int> list[10001]; //그래프 저장할 배열 int id[10001]; //방문할 순서를 저장할 배열 int seq = 1; //방문한 순서 int fin[10001]; //scc 여부 stack<int> s; vector<vector<int>> ans; //scc들을 저장할 배열 int dfs(int cur) { id[cur] = seq++; int ret = id[cur]; s.push(cur); for (int i = 0; i < list[cur].size(); i++) { int next = list[cur][i]; if (id[next] == 0) { //한번도 방문하지 않았다면 ret = min(ret, dfs(next)); //부모 중 가장 작은 id값을 ret에 저장 } else if (fin[next] == 0) { //방문했을 때 아직 scc가 아니라면 ret = min(ret, id[next]); //부모 중 가장 작은 id값을 ret에 저장 } } if (ret == id[cur]) { //부모 중 가장 작은 id값과 본인의 id값이 일치한다면 vector<int> scc; while (1) { int top = s.top(); //stack에서 빼주면서 fin[top] = 1; scc.push_back(top); //scc에 push s.pop(); if (top == cur) { //stack에서 본인을 만나면 break; } } sort(scc.begin(), scc.end()); ans.push_back(scc); } return ret; } int main() { cin >> V >> E; for (int i = 0; i < E; i++) { int a, b; scanf("%d %d", &a, &b); list[a].push_back(b); } for (int i = 1; i <= V; i++) { if(id[i] == 0) dfs(i); } sort(ans.begin(), ans.end()); printf("%d\n", ans.size()); for (int i = 0; i < ans.size(); i++) { for (int j = 0; j < ans[i].size(); j++) { printf("%d ", ans[i][j]); } printf("-1\n"); } } | cs |
'백준' 카테고리의 다른 글
| [ 백준 ] 2618번 - 경찰차 (C++) (0) | 2022.07.26 |
|---|---|
| [ 백준 ] 14938번 - 서강그라운드 (C++) (0) | 2022.07.25 |
| [ 백준 ] 1948번 - 임계경로 (C++) (0) | 2022.07.22 |
| [ 백준 ] 10830번 - 행렬 제곱 (C++) (0) | 2022.07.21 |
| [ 백준 ] 1786번 - 찾기 (C++) (0) | 2022.07.20 |