https://www.acmicpc.net/problem/14288
14288번: 회사 문화 4
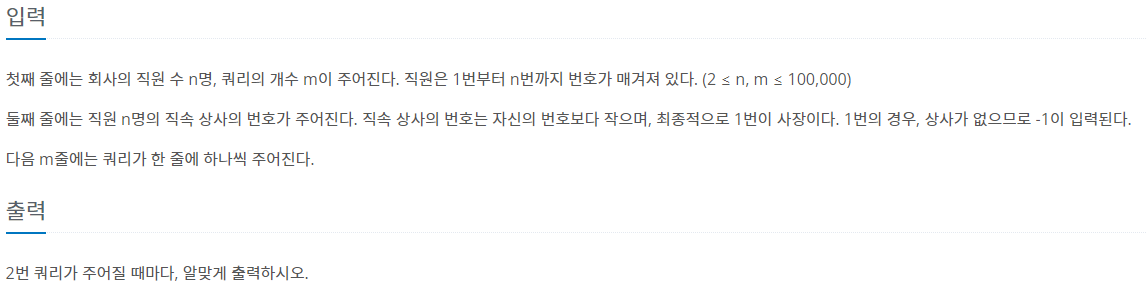
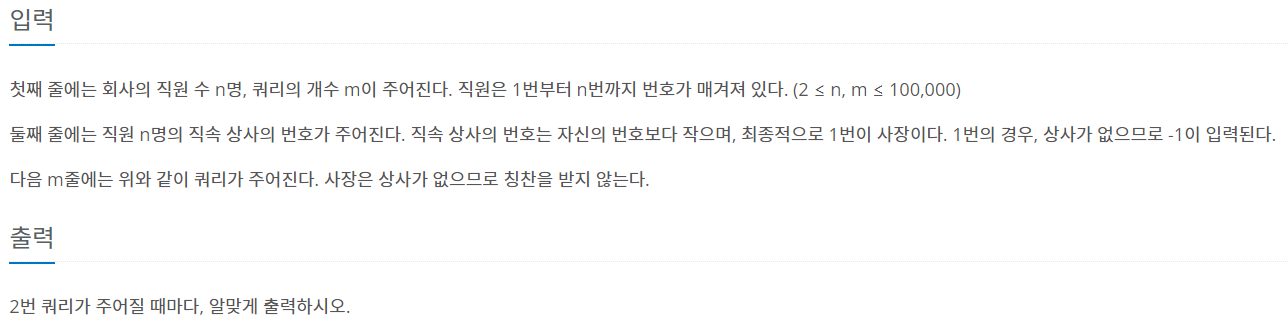
영선회사에는 매우 좋은 문화가 있는데, 바로 상사가 직속 부하를 칭찬하면 그 부하가 부하의 직속 부하를 연쇄적으로 칭찬하는 내리 칭찬이 있다. 즉, 상사가 한 직속 부하를 칭찬하면 그 부하
www.acmicpc.net

[ 문제풀이 ]
이 문제를 풀기 전에 다음 글을 먼저 읽고 오시는 것을 추천드립니다.
https://rudalsd.tistory.com/256
[ 자료구조 ] 느리게 갱신되는 세그먼트 트리 (Lazy Propagation)
https://rudalsd.tistory.com/51 [ 자료구조 ] 세그먼트 트리 (Segment Tree) 1. 세그먼트 트리 (Segment Tree) 먼저, 세그먼트 트리가 무엇인지 알아봅시다! 세그먼트 트리는 구간 합을 저장하기 위한 트리입니다.
rudalsd.tistory.com
1. dfs를 통해 각 노드가 몇 번에서 시작해서 몇 번에서 끝나는지 오일러 경로 테크닉을 이용하여 s[ n ], e[ n ]에 저장합니다.
2. 칭찬의 방향이 부하쪽이라면 느리게 갱신되는 세그먼트 트리를 이용하여 s[ i ]부터 e[ i ]까지 칭찬값을 더해줍니다.
3. 칭찬의 방향이 상사쪽이라면 비재귀 세그먼트 트리를 하나 더 만들어 n + s[ i ] 노드부터 1번 노드까지 칭찬값을 더해줍니다.
4. 느리게 갱신되는 세그먼트 트리에서 해당 인덱스의 값과 비재귀 세그먼트 트리에서 n + s[ i ]부터 n + e[ i ]까지의 구간 합을 더해 출력합니다.
[ 소스코드 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 | #include<iostream> #include<vector> using namespace std; int n, m; int s[100001]; int e[100001]; int cnt; int segTree[262222]; int lazy[262222]; int segTree2[200000]; vector<int> list[100001]; int cur = -1; int ans; void dfs(int num) { s[num] = ++cnt; for (int& next : list[num]) { dfs(next); } e[num] = cnt; } void updateLazy(int node, int l, int r) { if (lazy[node] != 0) { segTree[node] += lazy[node]; if (l != r) { lazy[node * 2] += lazy[node]; lazy[node * 2 + 1] += lazy[node]; } lazy[node] = 0; } } void updateTree(int node, int l, int r, int lidx, int ridx, int diff) { updateLazy(node, l, r); if (r < lidx || ridx < l) return; if (lidx <= l && r <= ridx) { if (l == r) { segTree[node] += diff; } else { lazy[node * 2] += diff; lazy[node * 2 + 1] += diff; } return; } int m = (l + r) / 2; updateTree(node * 2, l, m, lidx, ridx, diff); updateTree(node * 2 + 1, m + 1, r, lidx, ridx, diff); } void updateTree2(int node, int diff) { while (node != 0) { segTree2[node] += diff; node >>= 1; } } void getTree(int node, int l, int r, int idx) { updateLazy(node, l, r); if (idx < l || r < idx) return; if (l == r) { ans += segTree[node]; return; } int m = (l + r) / 2; getTree(node * 2, l, m, idx); getTree(node * 2 + 1, m + 1, r, idx); } void getTree2(int l, int r) { while (l <= r) { if (l & 1) { ans += segTree2[l]; l++; } if (~r & 1) { ans += segTree2[r]; r--; } l >>= 1; r >>= 1; } } int main() { scanf("%d %d", &n, &m); for (int i = 1; i <= n; i++) { int p; scanf("%d", &p); if (p != -1) { list[p].push_back(i); } } dfs(1); for (int j = 0; j < m; j++) { int com; scanf("%d", &com); if (com == 1) { int i, w; scanf("%d %d", &i, &w); if (cur == -1) { updateTree(1, 1, n, s[i], e[i], w); } else { updateTree2(n + s[i] - 1, w); } } else if (com == 2) { int i; scanf("%d", &i); ans = 0; getTree(1, 1, n, s[i]); getTree2(n + s[i] - 1, n + e[i] - 1); printf("%d\n", ans); } else { cur *= -1; } } } | cs |
'백준' 카테고리의 다른 글
| [ 백준 ] 2820번 - 자동차 공장 (C++) (0) | 2023.05.13 |
|---|---|
| [ 백준 ] 16404번 - 주식회사 승범이네 (C++) (0) | 2023.05.12 |
| [ 백준 ] 14287번 - 회사 문화 3 (C++) (0) | 2023.05.10 |
| [ 백준 ] 14268번 - 회사 문화 2 (C++) (0) | 2023.05.09 |
| [ 백준 ] 14267번 - 회사 문화 1 (C++) (0) | 2023.05.08 |