https://www.acmicpc.net/problem/12837
12837번: 가계부 (Hard)
살아있는 화석이라고 불리는 월곡이는 돈에 찌들려 살아가고 있다. 그에게 있어 수입과 지출을 관리하는 것은 굉장히 중요한 문제이다. 스마트폰에 가계부 어플리케이션을 설치해서 사용하려
www.acmicpc.net

[ 문제풀이 ]
이 문제를 풀기 전에 다음 글을 먼저 읽고 오시는 것을 추천드립니다.
https://rudalsd.tistory.com/51
[ 자료구조 ] 세그먼트 트리 (Segment Tree)
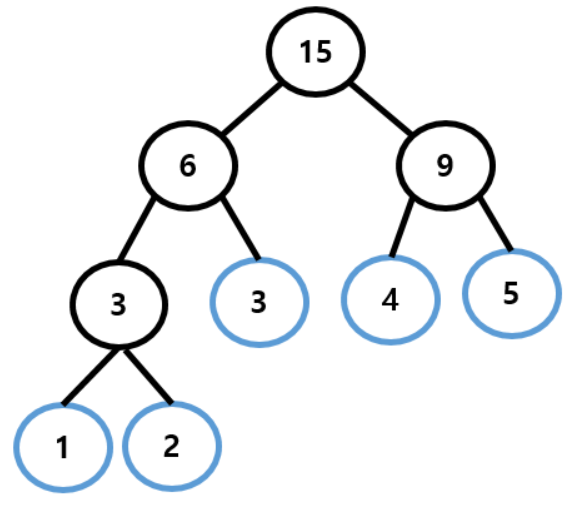
1. 세그먼트 트리 (Segment Tree) 먼저, 세그먼트 트리가 무엇인지 알아봅시다! 세그먼트 트리는 구간 합을 저장하기 위한 트리입니다. 예를 들어 size가 5인 배열이 있다고 생각해봅시다. int arr [5] = {1
rudalsd.tistory.com
1. 총합이 int형 범위를 벗어나므로 long long형으로 저장합니다.
[ 소스코드 ]
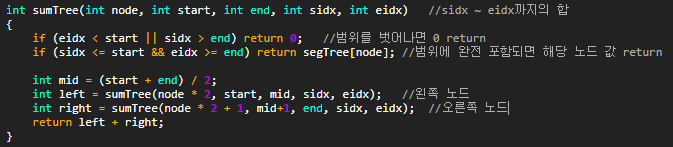
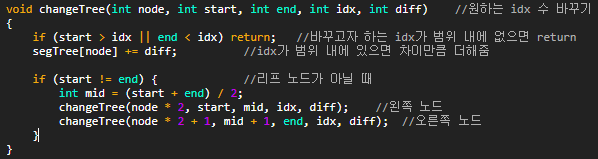
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | #include<iostream> #define ll long long using namespace std; int N, Q; ll segTree[2100000]; ll sumTree(int node, int start, int end, int sidx, int eidx) { if (end < sidx || start > eidx) return 0; if (sidx <= start && end <= eidx) return segTree[node]; int mid = (start + end) / 2; ll left = sumTree(node * 2, start, mid, sidx, eidx); ll right = sumTree(node * 2 + 1, mid + 1, end, sidx, eidx); return left + right; } void modifyTree(int node, int start, int end, int idx, ll x) { if (idx < start || idx > end) return; segTree[node] += x; if (start != end) { int mid = (start + end) / 2; modifyTree(node * 2, start, mid, idx, x); modifyTree(node * 2 + 1, mid + 1, end, idx, x); } } int main() { scanf("%d %d", &N, &Q); for (int i = 0; i < Q; i++) { int n, p, q; scanf("%d %d %d", &n, &p, &q); if (n == 1) { modifyTree(1, 1, N, p, q); } else { printf("%lld\n", sumTree(1, 1, N, p, q)); } } } | cs |
'백준' 카테고리의 다른 글
| [ 백준 ] 3745번 - 오름 (C++) (0) | 2023.01.03 |
|---|---|
| [ 백준 ] 14438번 - 수열과 쿼리 17 (C++) (0) | 2023.01.02 |
| [ 백준 ] 17244번 - 아맞다우산 (C++) (0) | 2022.12.31 |
| [ 백준 ] 17497번 - 계산 (C++) (0) | 2022.12.30 |
| [ 백준 ] 2268번 - 수들의 합 7 (C++) (0) | 2022.12.29 |